Лабораторная работа №5 Программирование циклических вычислительных процессов с использованием массивов и матриц.
Цель: Приобрести навыки программирования циклических вычислительных процессов с использованием массивов и матриц.
Теоретические разделы для выполнения лабораторной работы
- Особенности работы с массивами.
Программирование с использованием матриц.
Часть 1.
Программирование циклических вычислительных процессов с использованием массивов. Варианты заданий указаны в приложении 5, часть 1, с. 24.
Часть 2.
Программирование циклических вычислительных процессов с использованием матриц. Варианты заданий указаны в приложении 6, часть 2, с. 26.
Пример (Часть 1)
Дан массив а={a 1,a 2, …, a 15}. Найти модуль разности между максимальным и минимальным элементами массива.
Sub lr5_1()
Dim a(15),min, max, mod_raz, i As Integer
Dim s As String
S=””
For i=1 to 15
A(i)=Val(InputBox(“Элемент вектора”))
S=S & A(i) & “ “
Next i
MsgBox s , , “Введенный массив”
max=a(1)
min=a(1)
For i=2 to 15
If a(i)<min Then min=a(i)
If a(i)>max Then max=a(i)
Next i
mod_raz=abs(max-min)
MsgBox “Min = “ & min & “ Max=” & max & “Модуль разности =” & mod_raz
End Sub
Пример (Часть 2)
Задана матрица А размером 4X4. Сумму отрицательных элементов строки с наименьшим значением матрицы.
Sub lr5_1()
Dim a(4,4),min, i, j, imin, Sum_s As Integer
Dim s As String
S=””
For i=1 to 4
For j=1 to 4
A(i,j)=Val(InputBox(“Элемент матрицы”))
S=S & A(i,j) & “ “
Next j
S=S & Chr(13) & Chr(10)
Next i
MsgBox s , , “Введенная матрица”
min=a(1,1)
imin=1
For i=1 to 4
For j=1 to 4
If a(i,j)<min Then
min=a(i, j)
imin=i
End If
Next j
Next i
MsgBox “Min = “ & min & “ imin=” & imin
Sum_s=0
For j=1 to 4
If a(imin,j)<0 Then Sum_s=Sum_s + a(imin,j)
Next j
End Sub
Контрольные вопросы
-
Структура оператора цикла For … Next
- Использование вложенных операторов цикла
- Алгоритмы нахождение минимальных и максимальных значений
Работа с индексами массивов и матриц
Приложение 5. Варианты заданий лабораторной работы №5. Часть 1.
-
Найти минимальный и максимальный элементы вектора y ={ y 1 , y 2 ,…, y 10 } и поменять их местами.
- Задан вектор c ={ c 1 , c 2 , …, c n }. Найти вектор y ={ c 1 /| c |, c 2 /| c |, …, c n /| c |}, где | c | - длина вектора c.
- Даны два вектора x ={ x 1 , x 2 , …, x n } и y ={ y 1 , y 2 , …, y n }. Определить, ортогональны ли эти векторы.
- Найти косинус угла между двумя векторами a ={ a 1 , a 2 , …, a 20 } и b ={ b 1 , b 2 , …, b 20 }.
- Из двух векторов x ={ x 1 , x 2 , …, x 16 } и y ={ y 1 , y 2 , …, y 16 } определить тот, у которого больше длина.
- Найти сумму s положительных компонентов вектора b ={ b 1 , b 2 , …, b 15 }. Образовать новый вектор по формуле
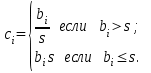
-
Заданы два вектора a ={ a 1 , a 2 , …, a n } и b ={ b 1 , b 2 , …, b n }. Определить тот из них, который имеет наименьшую длину.
- Найти наименьший из положительных элементов массива x ={ x 1 , x 2 , …, x 20 }.
- Найти наибольшее значение суммы x i + y i для массивов x ={ x 1 , x 2 , …, x 20 } и y ={ y 1 , y 2 , …, y 20 }.
- Даны векторы u ={ u 1 , u 2 , …, u 8 } и w ={ w 1 , w 2 , … w 8 }. Найти среднее арифметическое длин этих векторов.
- Вычислить сумму отрицательных и произведение положительных элементов вектора x ={ x 1 , x 2 , …, x 10 }. Найти длину этого вектора.
- Найти индексы наименьшего и наибольшего элементов вектора x ={ x 1 , x 2 , …, x 10 }. Определить их сумму S.
- Определить количество положительных элементов вектора x ={ x 1 , x 2 , …, x 20 }. Образовать новый вектор y из положительных элементов вектора x.
- Найти минимальный и максимальный элементы вектора y ={ y 1 , y 2 ,…, y 10 }. Вывести на экран их значения и индексы.
- Вычислить среднее арифметическое всех положительных элементов вектора x ={ x 1 , x 2 , …, x 20 }.
- Заданы векторы a ={ a 1 , a 2 , …, a n } и b ={ b 1 , b 2 , …, b n }. Найти скалярное произведение этих векторов.
- Даны векторы x ={ x 1 , x 2 , …, x 9 } и y ={ y 1 , y 2 , …, y 9 }. Найти количество положительных, отрицательных и нулевых элементов в каждом из этих векторов.
- Определить индекс наименьшего из положительных элементов вектора y ={ y 1 , y 2 , …, y 15 }.
- Даны векторы a ={ a 1 , a 2 , …, a 10 } и b ={ b 1 , b 2 , …, b 10 }. Найти sin угла между ними.
- Задан вектор a={a 1 , a 2 , …, a 8 }. Поменять его первый элемент с минимальным и последний a 8 – с максимальным.
- Определить индекс наибольшего из отрицательных элементов вектора y ={ y 1 , y 2 , …, y 15 }.
- Определить количество положительных элементов вектора x ={ x 1 , x 2 , …, x 20 }. Образовать новый вектор y из отрицательных элементов вектора x.
- Определить индекс наименьшего по модулю элемента вектора y ={ y 1 , y 2 , …, y 15 }.
- Даны два вектора x ={ x 1 , x 2 , …, x n } и y ={ y 1 , y 2 , …, y n }.Найти значение z=2· | x |– | y |, где | x |, | y |- длины векторов x, y.
- Вычислить среднее геометрическое всех положительных элементов вектора x={x 1 , x 2 , …, x 20 }.
- Даны два вектора x={x 1 , x 2 , …, x n } и y={y 1 , y 2 , …, y n }. Удалить из вектора x все нулевые элементы, а из вектора y все отрицательные.
- Дан вектор x={x 1 , x 2 , …, x n }. Найти z=sin(k)-cos(m), где k–максимальный по модулю элемент, m – минимальный элемент вектора.
- Найти наибольший из положительных элементов массива x ={ x 1 , x 2 , …, x 20 } и количество отрицательных элементов..
- Дан вектор x ={ x 1 , x 2 , …, x n }. Найти: сумму элементов больших 10, произведение отрицательных элементов и наибольший по модулю элемент вектора.
Даны векторы a ={ a 1 , a 2 , …, a 10 } и b ={ b 1 , b 2 , …, b 10 }. Найти косинус угла между ними и количество элементов вектора равных нулю.
Приложение 6. Варианты заданий лабораторной работы №5. Часть 2.
-
Дано натуральное число n. Получить действительную матрицу [аij ]
i,,j=1,…, n, для которой
а
ij =
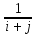 ; Найти количество отрицательных элементов матрицы
; Найти количество отрицательных элементов матрицы
-
Дано натуральное число n. Получить действительную матрицу [аij ]
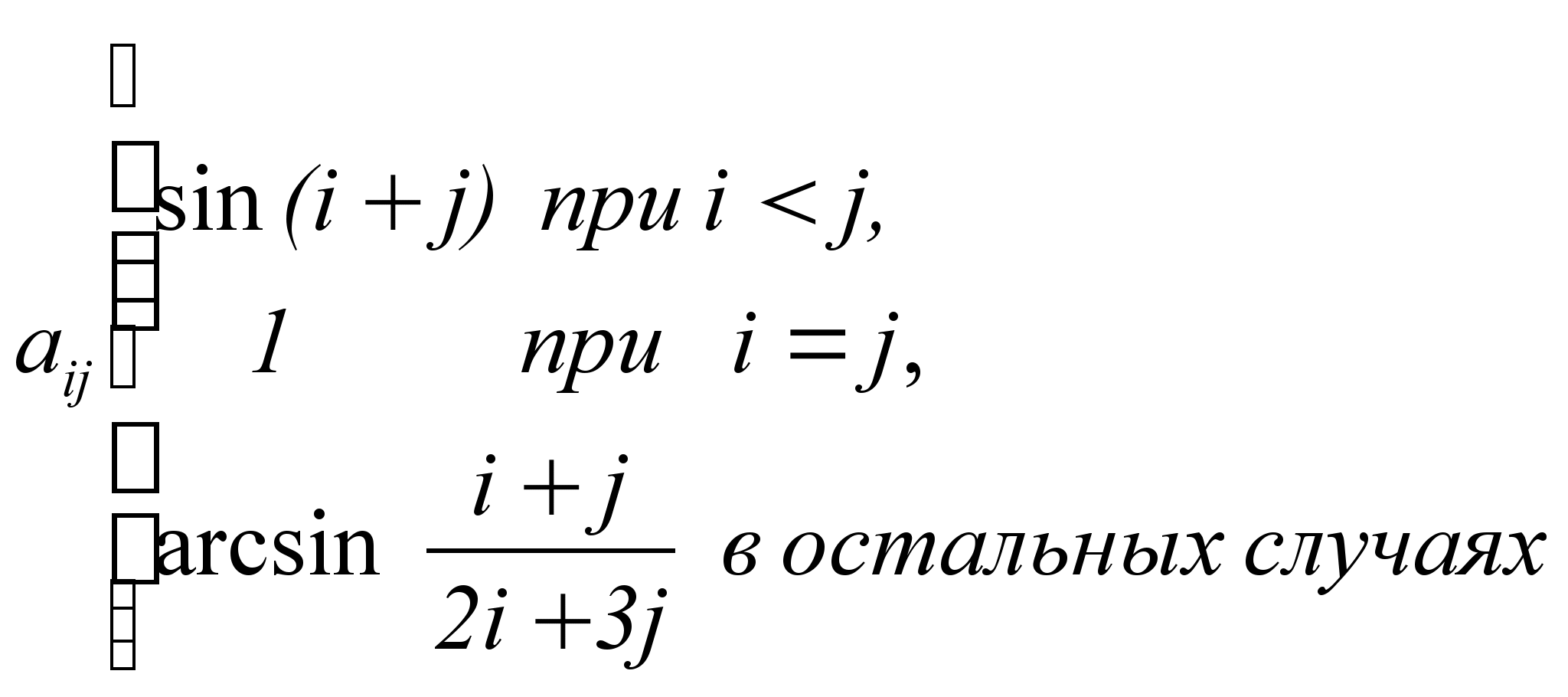 i , j=1,…, n, для которой
i , j=1,…, n, для которой
Найти количество отрицательных элементов матрицы
-
Дана действительная квадратная матрица [аij ] i , j =1,…, n . Получить две квадратные матрицы
[b ij ] i , j =1,…, n , [с ij ] i , j =1,…, n , для которых
bij =
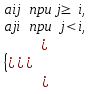 сij =
сij =
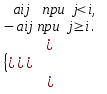
-
Получить действительную матрицу [аij ] i , j =1,…, 7, первая строка которой задается формулой
а1j = 2j+3 ( j = 1, … ,7 ),
вторая строка задается формулой а2j = j
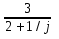 ( j = 1, …, 7 ), а каждая следующая строка есть сумма двух предыдущих.
( j = 1, …, 7 ), а каждая следующая строка есть сумма двух предыдущих.
-
Даны натуральное число n , действительная матрица размера n х 9. Найти среднее арифметическое:
а) каждого из столбцов;
б) каждого из столбцов, имеющих четные номера.
-
Дано натуральное число n. Выяснить, сколько положительных элементов содержит матрица [аij ] i , j =1,…, n, если
аij = cos (
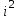 + n);
+ n);
-
Дана действительная матрица размера n х m, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на её наибольший по модулю элемент.
- Даны натуральное число m , целые числа а1, ……. , аm и целочисленная квадратная матрица порядка m . Строку с номером i матрицы назовем отмеченной , если аi > 0, и неотмеченной в противном случае.
а) Подсчитать число отрицательных элементов матрицы, расположенных в отмеченных строках.
б) Нужно все элементы , расположенные в отмеченных строках матрицы , преобразовать по правилу: отрицательные элементы заменить на –1, положительные – на 1 , а нулевые оставить без изменения.
-
Дана действительная квадратная матрица порядка 12. Заменить нулями все ее элементы , расположенные на главной диагонали и выше нее.
- Даны действительные числа Х1, …., Х8. Получить действительную квадратную матрицу порядка 8:

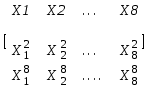
-
Дана действительная матрица размера m х n.
Определить числа b1, … ,bm , равные соответственно:
а) произведениям элементов строк;
б) наименьшим значениям элементов строк ;
в) значениям средних арифметических элементов строк ;
г) разностям наибольших и наименьших значений элементов строк.
-
Все элементы с наибольшим значением в данной целочисленной квадратной матрице порядка 10 заменить нулями.
- Дана действительная матрица размера 6 х 9 . Найти среднее арифметическое наибольшего и наименьшего значений ее элементов.
- Дана действительная матрица размера 18 х n . Найти значение наибольшего по модулю элемента матрицы, а также индексы какого-нибудь элемента с найденным значением модуля.
- Дана действительная матрица размера m х n . Найти сумму наибольших значений элементов ее строк.
- В данной действительной квадратной матрице порядка n найти сумму элементов строки , в которой расположен элемент с наименьшим значением . Предполагается , что такой элемент единственный.
- В данной действительной матрице размера 6 х 9 поменять местами строку , содержащую элемент с наибольшим значением , со строкой , содержащей элемент с наименьшим значением. Предполагается , что эти элементы единственны.
- Дано натуральное число n. Выяснить, сколько отрицательных элементов содержит матрица [аij ] i , j =1,…, n, если
аij = sin (i+j/2);
-
Даны натуральное число n , действительная квадратная матрица порядка n , действительные а1,…, аn+5
Элементы последовательности а1,…, аn+5 домножить на 10 ,если наибольший элемент матрицы (в предположении, что такой элемент единственный ) находится на главной диагонали , и на 0.5 в противном случае.
-
В данной квадратной целочисленной матрице порядка 17 указать индексы всех элементов с наибольшим значением.
- Дана действительная матрица размера m х n. Определить числа b1, … ,bm, равные соответственно:
а) наименьшим значениям элементов строк ;
б) значениям средних арифметических элементов строк ;
в) разностям наибольших и наименьших значений элементов строк.
-
Дана действительная матрица размера m х n, все элементы которой различны . В каждой строке выбирается элемент с наименьшим значением , затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.
- Дана действительная матрица размера m х n.Получить последовательность b1 ,…, bn , где br –это
а) наибольшее из значений элементов r-й строки ;
б) сумма наибольшего и наименьшего из значений элементов r-й строки ;
в) число отрицательных элементов r-й строке ;
г) произведение квадратов тех элементов r-й строки , модули которых принадлежат отрезку [1, 1.5].
-
Дана целочисленная квадратная матрица порядка 8 . Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько ,то взять первый из них.
- Даны натуральное число n , целочисленная квадратная матрица порядка n. Получить b1 ,…, bn , где bi- это
а) наименьшее из значений элементов , находящихся в начале i – й строки матрицы до элемента , принадлежащего главной диагонали , включительно:
б) значение первого по порядку положительного элемента i – й строки (если таких элементов нет , то принять bi=1);
в) сумма элементов , расположенных за первым отрицательным элементом в i – й строке (если все элементы строки неотрицательны , то принять bi = 100) ;
г) сумма элементов i – й строки (если все элементы строки неотрицательны ,то принять bi = -1 ).
-
Дана целочисленная квадратная матрица порядка n . Найти номера строк:
А) элементы которых – нули ;
Б) элементы в каждой из которых одинаковы ;
В) все элементы которых четны ;
Г) элементы каждой из которых образуют монотонную последовательность (монотонно убывающую или монотонно возрастающую);
-
Даны натуральное число n , действительное число х , действительная матрица размера n х 2 n. Получить последовательность b1 ,…, bn из нулей и единиц , где bi=1, если элементы i– й строки матрицы не превосходят х , и bi=0 в противном случае.
- Дана действительная квадратная матрица порядка 10 . В строках с отрицательным элементом на главной диагонали найти:
А) сумму всех элементов;
Б) наибольший из всех элементов.
-
Дано натуральное число n. Выяснить, сколько положительных элементов содержит матрица [аij ] i , j =1,…, n, если
аij = sin
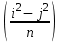 .
.
CC-BY-CA Анатольев А.Г., 31.01.2012